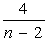Definition - "Polygon" is a Greek word meaning "many sides." The regular polygon is a convex plane shape (fills a flat surface) which has all of its sides the same length, and all its internal angles the same size. There are an infinite number of these. We will investigate some of the properties of these shapes below.
Activity A:
In this activity we will find the relationship between the number of sides of a polygon and its internal angles. To do this you should use the first four regular polygons to complete the table below. After you have completed the pentagon and hexagon rows you should try to find a pattern. Then complete the last row for a polygon of n sides.
- In the second column write the number of sides in each polygon.
- In the third column write the number of non-overlapping internal triangles which can be drawn inside the polygon.
- In the fourth column write the sum of all the internal angles in each polygon. Remember that the sum of the internal angles of a triangle is 180 degrees, so you should multiply the number of triangles (in column three) by 180.
- In the last column write the size of the internal angle at each vertex. To do this divide the sum of angles (in column four) by the number of sides (in column two).
I have completed the first two rows as an example.
| Polygon | Sides |
Internal Triangles | Sum of
internal angles |
Internal Angles |
 | 3 | 1 |
1x180 = 180 | 180/3 = 60 |
 | 4 | 2 |
2x180 = 360 | 360/4 = 90 |
 | 5 | |
| |
 | 6 | |
| |
| n - sided | n | |
| |
Activity A - Answer
Activity B:
In this activity we will investigate which regular polygons "fill the plane at a point" or tessellate the plane.
Firstly, we will use the diagram below to help.
|
|
- Click on one of the polygon buttons to begin.
- Click on the red dot inside the polygon shape and drag it so that one of the polygon's vertices touches the red dot in the centre of the page. Now click the 'Next>>' button.
- Continue to do this, placing each new polygon's vertex on the red dot, with its side touching another polygon.
- Rotate the polygon clockwise by pressing "C" and anti-clockwise by pressing the "A" key on your keyboard.
- See if the polygons can fit evenly together at the red dot.
- Repeat this for the other polygons.
|
Question 1.
Complete this sentence, summarising your findings: "The shapes ..............., ............., and ............... fill the plane at a point".
Question 1 - Answer
Question 2.
Look at the internal angles of each of the regular polygons which "fill the plane at a point". Use these angles to explain why these shapes "fill the plane" but the pentagon and heptagon don't?
Question 2 - Answer
Question 3.
Do you think that any other polygons will "fill the plane at a point"? Make a conjecture . Try to prove your conjecture for all regular polygons.
Question 3 - Answer
Answer Activity A
| Polygon | Sides |
Internal Triangles | Sum of
internal angles |
Internal angles |
 | 3 | 1 |
1x180 = 180 | 180/3 = 60 |
 | 4 | 2 |
2x180 = 360 | 360/4 = 90 |
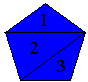 | 5 | 3 |
3x180 = 540 | 540/5 = 108 |
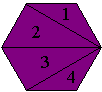 | 6 | 4 |
4x180 = 720 | 720/6 = 120 |
| n-sided | n | n-2 |
(n-2)x180 | (n-2)x180/n |
Back
Answer Question 1
My summary reads "The shapes equilateral triangle, square, and hexagon "fill the plane at a point".
Back
Answer Question 2
I notice that all the shapes which "fill the plane" have internal angles (60, 90, 120) which divide evenly into 360 degrees. The pentagon and heptagon have internal angles (108, 900/7) which don't divide evenly into 360 degrees.
Back
Answer Question 3
My conjecture is: "Only the equilateral triangle, square, and hexagon "fill the plane at a point".
I have come to this conclusion because:
We have tested the five polygons and found that the equilateral triangle, square, and hexagon work. This is because their internal angles are factors of 360 degrees (the size of the revolution angle at the point).
That is, it takes exactly six 60 degree angles (equilateral triangle) to make 360 degrees, and exactly four 90 degree angles (square) to make 360 degrees, and exactly three 120 degree angles (hexagon) to make 360 degrees. The pentagon doesn't "fill the plane" because its internal angle (108 degrees) doesn't divide evenly into 360, so more than three but less than four are needed.
Now, the remaining regular polygons have more than 6 sides. They will need less than 3 shapes to fill the plane if the hexagon took exactly 3. But this means that two are needed (or the trivial "one"), which means that the internal angles have to be 180 degrees - a straight line! So no other regular polygons will "fill the plane at a point"
Below is a different proof for my conjecture for those readers who know algebra.
We said above that the internal angle of a regular n sided polygon can be found by using the formula:
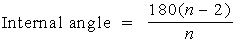 .
.
The only way that the n sided polygon can "fill the plane" is if 360 degrees can be divided evenly by the internal angle. Let the result of this division for a polygon which "fills the plane" be the whole number w.
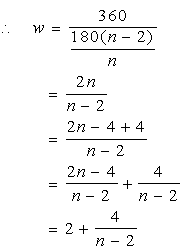
Now 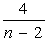 must be a whole number. We can make a table to see the possible solutions for n.
must be a whole number. We can make a table to see the possible solutions for n.
| n | 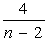 |
| 3 | 4 |
| 4 | 2 |
| 5 | |
| 6 | 1 |
From ths table we can see that the only possible whole number values for n are 3, 4, and 6.
Q.E.D.
Back









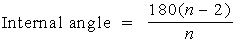 .
. 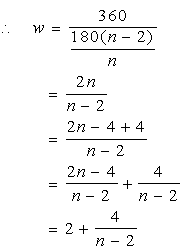
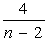 must be a whole number. We can make a table to see the possible solutions for n.
must be a whole number. We can make a table to see the possible solutions for n.