Pythagoras of Samos

Return to MENU
Back
PYTHAGORAS of SAMOS
A Collection of Essays and Lessons for Junior and Senior High School

Contents
4. Pythagoras' Theorem - origins and proofs
5. Plimpton 322 - Babylonian clay tablet
6. Academic

Pythagoras' Theorem

You might like to do Activity 2 before you continue.

Background

Firstly, we need to appreciate that Pythagoras did not discover the relationship between the length of the sides of a right-angled triangle. This relationship had been known in Babylon and Egypt for centuries (if not millennia) before. Tradition has it though, that Pythagoras did find the first rigorous geometric proof. I will digress to describe an extraordinary clay tablet containing evidence of Babylonian knowledge of the relationship, at the end of this essay. Numerical relationship I would like to start my discussion on Pythagoras' Theorem not with geometry, but with number patterns as this is the method used by Pythagoras according to Proclus (410-485 A.D.) (cited in Heath [4]):

"Certain methods for the discovery of triangles of this kind are handed down, one of which they refer to Plato, the other to Pythagoras. [The latter] starts from odd numbers. For it makes the odd number the smaller of the sides about the right angle; then it makes the square of it, subtracts unity, and makes half the difference the greater of the sides about the right angle; lastly it adds unity to this and so forms the remaining side the hypotenuse. For example, taking 3, squaring it, and subtracting unity from the 9, the method takes half of the 8, namely 4; then, adding unity to it again, it makes 5, and a right-angled triangle has been found…"

This method will yield Pythagorean triples (whole numbers which can form the lengths of a right angled triangle), but it does not yield all triples. It should be seen that the problem of finding Pythagorean triples is to find two square numbers such that their sum is also a square.

One possible way that Pythagoras may have arrived at triples is through the use of the gnomon. The gnomon is the name given to the oblique staff which is used to cast a shadow in the sundial. It is claimed that Anaximander, a contemporary to Pythagoras, introduced the gnomon to Greece from Babylon. As we will see soon,the gnomon became synonymous with the numbers formed by the difference between successive squares - the odds. We know that Pythagoras investigated the figurate numbers and their related patterns. He would possibly have represented the consecutive square numbers 1, 4, 9, 16, 25 as stones grouped as in the figure (figure 2A) below:

With a bit of inspection, one can see that to make 4 from 1, only takes the addition of the "L" shaped (gnomon) figure of three stones. To make 9 from 4 the gnomon is made up of the next consecutive odd number, 5. If you continue investigating this pattern you will eventually arrive at a shape where the gnomon is also square i.e. 16 + 9 = 25; the first Pythagorean triple.

A related, but more abstract and therefore less likely, way that the relationship may have been seen is by writing down three rows of numbers (a) the counting numbers, (b) their squares and (c) the successive odd numbers constituting the difference between the successive squares (figure 2B). By picking out the numbers in the third row which are squares, Pythagoras would have arrived at the same point as above.

Counting Numbers	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Squares	1	4	9	16	25	36	49	64	81	100	121	144	169	196
gnomon	3	5	7	9	11	13	15	17	19	21	23	25	27

figure 2B

It would seem unlikely that Pythagoras would use this device because Burnet argues there is no evidence to suggest that the concept of number had progressed much more than as a collection of pebbles at this time. It is only over the next few centuries that the Pythagoreans developed an abstracted number sense which would allow a representation as above.

It is worth noting that neither method would expose the incommensurables (the irrational numbers) and neither is useful as a general proof of the theorem.

Geometrical proof Whether the relationship was taught to him, or whatever method Pythagoras used to find triples, it is generally accepted that he was the first to give a general proof for the relationship. Heath claims that the proof given in Proposition 47, Book I of Euclid's Elements is generally attributed to Euclid and makes use Propositions not known to Pythagoras. He goes on to describe the following proof using similar triangles and proportion as one most probably used by Pythagoras:

"One method is to prove, from the similarity of triangles ABC, DBA, that the rectangle CB,BD is equal to the square on BA, and, from the similarity of the triangles ABC, DAC, that the rectangle BC,CD is equal to the square on CA; whence the result follows from addition"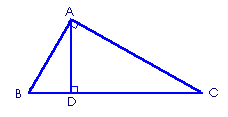
Notice how the product of CB and BD is described as "the rectangle CB,BD". This is how the early Pythagoreans understood multiplication - as a physical area (as apart from an abstract product). In modern courses this same explanation would be:

Which is the familiar theorem. Click this link to see a Pythagoras' Theorem joke

There are many different proofs and demonstrations for this theorem of Pythagoras'. Below is a particularly nice demonstration.

Drag the red dot to form the moveable areas.
Press "Define" button.
Then drag the red dots to reform the areas in the clear square.
Press "Init" button.

Plimpton 322 (1900 B.C.E. - 1600 B.C.E.) This century, archeologists have unearthed close to half a million Babylonian clay tablets. Of these over 300 have been identified as purely mathematical tables. One such tablet, called Plimpton 322 (so called because it is item number 322 in the G.A. Plimpton collection at Columbia University) is of special interest to this essay (figure 2C).

figure 2C
At first glance, when the cuneiform is translated to our numerals, (figure 2D) the table looks like another record of business transactions, stocktaking etc. Analysis however, shows that it has a deep mathematical significance in the theory of numbers.

Howard Eves [5] describes the tablet as having three essentially complete columns of figures as reproduced below in figure 2D (only part of the tablet is reproduced here as illustration).

figure 2D
He states that the column on the far right merely numbers each of the lines, and then shows how the other two columns are the hypotenuse and leg of integral-sided right triangles (with a couple of errors - in brackets). He asserts that there is some evidence (considering the properties of the sexagesimal numbers present), to support the view that the Babylonians at this time were aware of the parametric formula for finding the primitive Pythagorean triples.

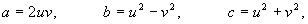
All primitive ( i.e. no common ratio between the three - 6,8,10 is not a primitive triple) Pythagorean triples (a,b,c) are given parametrically by:

where u and v are relatively prime, one is odd while the other is even (that is they have different parity), and u > v. Thus if u = 2 and v = 1, we get the primitive triple a = 4, b = 3, c= 5.
Eves then goes on to show how the values on the tablet could have been produced:

a	b	c	u	v
120	119	169	12	5
3456	3367	4825	64	27
4800	4601	6649	75	32
13500	12709	18541	125	54
72	65	97	9	4
360	319	481	20	9
2700	2291	3541	54	25
960	799	1249	32	15

Needless to say, if the conclusion made in Eves is correct, then there is evidence of the Pythagorean relationship being known in Babylonia over 1000 years before Pythagoras. Of course no rigorous proof is forthcoming from this period.

On to Pythagorean beliefs about Number

References:

[4] Heath, Sir Thomas L., Euclid - The Thirteen Books of The Elements Second Edition Vol i, N.Y.: Dover Publications (orig 1908) On-line version with java applet

[5] Eves, Howard, An Introduction To The History of Mathematics 5th Ed., N.Y.: Saunders College Publishing, 1983

[6] This Essay and the related classroom Activities are on-line at MATHGYM ( http://www.mathtrak.com.au/mic/ )