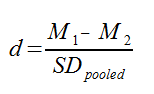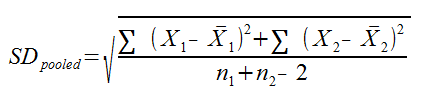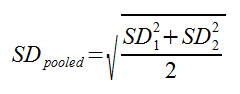MATHTRAK's researchMATHTRAK has compared the test performance of each of approximately 150 students in 6 courses over three years in a secondary school with their progress with school-set questions based on the course at MATHTRAK. Over this time each student has used MATHTRAK by varying degrees from not at all through to getting 100% success at MATHTRAK prior to the exam. The research was conducted to determine if a student's test performance improves with increased use and success with MATHTRAK.MethodFor each of the six course assessments, each student's test perfomance on Knowledge was converted to a z-score (between -3 and 3) and their attempts on, and success with MATHTRAK questions was calculated (on a scale of 0 to 1). this time a of using ) has found that when a student successfully completed greater than 75% of MATHTRAK quizzes 25% of MATHTRAK progress (mean: -0.271702615776571 , SD: 0.993650502226584) compared to those in the upper 25% of MATHTRAK progress (mean: 0.494751651024253 , SD: 0.718661603433932) is 0.88.Effect Size and John HattieIn Visible Learning John Hattie suggests that an effect size of -0.1 - 0.16 is what a student would learn if not in a classroom; an effect size of 0.16 - .4 would be the effect of a normal classroom. He states that an effect size of 0.40 is about the average effect we expect from a year?s schooling. Therefore interventions of 0.40 and above are the ones that will truly improve student achievement. It has also been claimed that an effect size of 0.5 is equivalent to a one grade leap at GCSE and an effect size of 1.0 is equivalent to a two grade leap at GCSE.Determining Effect Size using Cohen's dCohen’s d is a measure of the distance between two means, measured in standard deviations. The formula used to calculate the Cohen’s d looks like this:
Where M1 and M2 are the means for the 1st and 2nd samples, and SDpooled is the pooled standard deviation for the samples. SDpooled is properly calculated using this formula: In practice, though, you don’t necessarily have all this raw data, and you can typically use this much simpler formula:
|