Back
Activity 4 - Finite Differences and Inductive Proof
This Activity and the related Essays on the History of Mathematics are on-line at MATHGYM (http://www.mathtrak.com.au/mic/)
In this activity you will learn both a method for finding the equation given a table of related numbers, and for proving that the equation is correct using the technique of Mathematical Induction. To fully appreciate this Activity you need some understanding of elementary algebra.
Figurate Numbers
It is trivial to find the nth term of the square numbers (the 10th term is 102 = 100 ) but it is not so clear how to get the formula for the nth term of the triangular numbers. There is a useful method called "finite differences" which we can use and I will try to explain how it works below for you. It is somewhat complex so bear with me as it is also pretty powerful (and nifty).
We now add a third column called the "first differences". In this column we place the difference between each consecutive number in the sequence. For example the first two terms are 1 and 3 so the difference is 2 ; the next pair of terms is 3 and 6 with a difference of 3.
You should stop at this stage and check the values in the "first differences" column. If they happen to be a constant ( i.e. all of them the same - 1 or 23 or something ) then the relationship between the values is linear. That is the formula is of the form y = mx+c.
By now you have noticed that all the values in the "second differences" column are a constant ( 1 ). Whenever this happens we know that the relationship is quadratic . That is the formula is of the form
1. First of all we add another column which contains some multiple of tn. Which multiple of tn we put in this column depends on the constant in the "second differences" column. If the constant is 2 we simply repeat each value in the tn column. If the constant isn't 2, we work out what we have to multiply the constant by to get the value of 2. In our example, the constant in the "second differences" column is 1 so we have to multiply by 2. So in our new column we put 2 times each of the values in the tn column. This is shown below:
2. Next we add another column which is the result of the difference between that last column ( in this case 2tn ) and n2:
3. At this stage we would do our differences again to find the linear equation equal to 2tn - n2. But with this example we can see that the values in the 2tn - n2 column are identical to the values in the (n) column. This means that:
For your interest, if it takes three differences to get a constant than the relationship is a cubic of the form:
See if you can find the equation for finding the nth term in the pentagonal numbers.
1 = 1
A clear pattern emerges in the sums 1, 4, 9, 16, 25, 36; they are the squares of the natural numbers l, 2, 3, 4, 5, 6. We can generalise our observation by making the conjecture: "The sum of the first n odd positive integers is equal to n2, or, stated in symbols,
1 + 3 + 5 + 7 + ...+ (2n-1) = n2
Let us be clear about this way of writing a general equation. The nth odd number can be written generally as 2n-1. The "+...+" means "continue this pattern". So this equation reads "the sum of the first n consecutive odd numbers is n squared"
Is the pattern a proof of our conjecture? No it isn't. We have already established that a few correct examples doesn't prove a general formula, because the next example we try might be a contradiction. Perhaps the easiest way to prove that a general formula of the type above is valid for every positive integer n, is to use mathematical induction.
The Principle of Mathematical Induction
To explain the principle behind mathematical induction I like to think of a row of dominos all standing on their ends
How can we prove the conjecture: "For any equally spaced row of dominos, the last domino will fall if the first one is pushed over"? Let us start by putting two dominos up, then three, then four, etc. and test them to see if they all fall. We start with the simplest case - that of two dominos. If the distance between them is correct, both will topple. We will call this case D1.
Next we look at the second case (of three dominos), D2:
Once again, if the distances are the same as in D1 then the third domino will fall. We continue like this testing each of the third case D3, the fourth D4, and so on. Since I don't know how many dominos there are in total I will call the last case, where there are n+1 dominos that fall the Dn th case.
If we are to prove the general case then we have to test for every case. Let us start with the first five cases (D1,D2,D3,D4,D5). We can test these by physical trial and find that these work if they are set up properly. The conjecture actually comprises the infinitely many cases " D1 will fall, D2 will fall, D3 will fall,..." . So far, we have seen only that D1,D2,D3,D4,D5 fall and we want to establish that all of (infinitely many) of these cases will fall before we actually test them.
The principle of mathematical induction states that we can establish the truth of any such infinite sequence of cases if we can prove two results:
So if we prove 1 we will have a start on this chain, and the case of D1,D 2, D3, D4, and so on, will follow on from the case of D1 by 2.
We can tell by actual calculation that all six statements are true. The conjecture "Pn is true for every positive integer n" actually comprises the infinitely many assertions "P1 is true, P2 is true, P3 is true,..." . So far, we have seen only that P1, P2, P3, P4, P5, P6 are true and we want to establish the truth of all (infinitely many) of these cases. Here is how we use Induction:
Pk + (2k+1) = 1 + 3 + 5 + 7 +...+ (2k-1) + (2k+1) = k2 + (2k+1)
See if you can prove the Conjecture - 1 + 2 + 3 + 4 + ... + n = (n2+n)/2 by mathematical induction. This is also the formula for the nth term of the triangular numbers.
See if you can prove the Conjecture - 1 + 4 + 7 +...+ (3n-2) = (3n2-n)/2 by mathematical induction. This is also the formula for the nth term of the pentagonal numbers.
Figurate Number Geometric shape triangular numbers 
square numbers 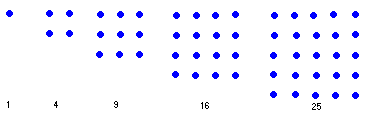
pentagonal numbers 
term
(n) nth term
(tn) 1 1 2 3 3 6 4 10
term
(n) nth term
(tn) 1st
diff. 1 1 2 2 3 3 3 6 4 4 10
The numbers in our pattern aren't constant so we go to the next step. Next we add a fourth column called the "second differences". In this column we place the difference between each consecutive number in the "first differences" column. For example the first two values are 2 and 3 so the difference is 1 ; the next pair of values are 3 and 4 with a difference of 1 also.
term
(n) nth term
(tn) 1st
diff. 2nd
diff. 1 1 2 2 3 1 3 3 6 1 4 4 10
y = ax2+bx+c .
It only remains for us to find the quadratic equation.
We do this by extending the table in the following way:
term
(n) nth term
(tn) 1st
diff. 2nd
diff. 2tn 1 1 2 2 2 3 1 6 3 3 6 1 12 4 4 10 20
term
(n) nth term
(tn) 1st
diff. 2nd
diff. 2tn 2tn - n2 1 1 2 1 2 2 3 1 6 2 3 3 6 1 12 3 4 4 10 20 4
2tn - n2= n
<=> 2tn = n2 + n
<=> tn = ( n2 + n )/2
And this is the formula for the nth term of the triangular numbers!
y = ax3 + bx2 + cx + d. If the constant is equal to 6 the value of tn is unchanged. You continue to use the process above to find the equation.
Question 1:
In a previous essay we investigated the discovery made by the early Pythagoreans about the relationship between the gnomon and the square numbers. This relationship can be viewed in another form - the sum of consecutive odd numbers:
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 + 5 + 7 + 9 + 11 = 36




D1 works
D1 will cause D2,
D2 will cause D3,
D3 will cause D4,
D4 will cause D5,
and so on.
All we need do is set up the two dominos at the correct separation and push the first one over. If the second falls then know that D1 works.
The key to whether all the dominos fall is in the separation between each domino. If the separation between any pair of dominos is the same as the separation in D1, then any falling domino will strike the next domino in line which should also fall. Let us assume that somewhere in the row a domino is falling and that this "falling domino" is the last domino in case Dk. Since Dk works then the last domino of Dk will fall against the next domino in line which will also fall. This is case Dk+1 which works because Dk works. So we have established that D1 is true, and that if one of the cases is true so is the next one which means that D2 is true. But this means that D3 is true ..., which means that Dn is true. Which proves, by induction that all the dominos will fall.
Let us call Pn = 1 + 3 + 5 + 7 + ...+ (2n-1) = n2 so that:
P1 =1 = 1
P2 =1 + 3 = 4
P3 =1 + 3 + 5 = 9
P4 =1 + 3 + 5 + 7 = 16
P5 =1 + 3 + 5 + 7 + 9 = 25
P6 =1 + 3 + 5 + 7 + 9 + 11 = 36
Thus Pk+1 follows from Pk. We have established that if any one of the cases ( Pk) is true so is the next one (Pk+1). We also proved that P1 is true, which means that P2 is true. But this means that P3 is true ... , which means that Pn is true, which is the proof of our conjecture by mathematical induction.
This is not difficult since P1 is simply 1 = 1.
If the conjecture is true then
Pk = 1 + 3 + 5 + 7 +...+ (2k-1) = k2
and
Pk+1 = 1 + 3 + 5 + 7 +...+ (2k+1) = (k+1)2
What we have to do is, starting with Pk show that Pk+1 follows as a consequence.
To get Pk+1 from Pk, we have to add on the next odd number after (2k-1), so let us add (2k+1) to both sides of the equation Pk:
= k2 + 2k + 1
= (k+1)2
= Pk+1
Question 2:
Question 3:
Answer Question 1
| term (n) | nth term (tn) | 1st diff. | 2nd diff. | (2/3)tn | (2/3)tn - n2 |
| 1 | 1 | 2/3 | -1/3 | ||
| 4 | |||||
| 2 | 5 | 3 | 10/3 | -2/3 | |
| 7 | |||||
| 3 | 12 | 3 | 8 | -1 | |
| 10 | |||||
| 4 | 22 | 3 | 44/3 | -4/3 |
From the table we can see that the values in the column (2/3)tn - n2 are identical to negative one third times the values in the (n) column. This means that:
(2/3)tn - n2= (-1/3)n
<=> 2tn - 3n2 = -n
<=> tn = (3n2 - n )/2
And this is the formula we wanted to find!
Answer Question 2
Let Pn = 1 + 2 + 3 + 4 + ... + n = (n2+n)/2
Pk + (k+1) = 1 + 2 + 3 + 4 +...+ k + (k+1) = (k2+k)/2 + (k+1)
Let Pn = 1 + 4 + 7 + 10 + ... + (3n-2) = (3n2-n)/2
Pk + (3k+1) = 1 + 4 +...+ (3k-2) + (3k+1) = (3k2-k)/2 + (3k+1)
Thus Pk+1 follows from Pk. We have established that if any one of the cases ( Pk) is true so is the next one (Pk+1). We also proved that P1 is true, which means that P2 is true. But this means that P3 is true ... , which means that Pn is true, which is the proof of our conjecture by mathematical induction.
This is not difficult since P1 is simply 1 = 1.
If the conjecture is true then
Pk = 1 + 2 + 3 + 4 + ... + k = (k2+k)/2
and
Pk+1 = 1 + 2 + 3 + 4 + ... + k+1 = ((k+1)2+(k+1))/2 = (k2+3k+2)/2
What we have to do is, starting with Pk show that Pk+1 follows as a consequence.
To get Pk+1 from Pk, we have to add on the next number after k, so let us add (k+1) to both sides of the equation for Pk:
= (k2+k+2k+2)/2
= (k2+3k+2)/2
= Pk+1
Answer Question 3
Thus Pk+1 follows from Pk. We have established that if any one of the cases ( Pk) is true so is the next one (Pk+1). We also proved that P1 is true, which means that P2 is true. But this means that P3 is true ... , which means that Pn is true, which is the proof of our conjecture by mathematical induction.
This is not difficult since P1 is simply 1 = 1.
If the conjecture is true then
Pk = 1 + 4 + 7 + 10 + ... + (3k-2) = (3k2-k)/2
and
Pk+1 = 1 + 4 + 7 + 10 + ... + (3k+1) = (3(k+1)2-(k+1))/2 = (3k2+5k+2)/2
What we have to do is, starting with Pk show that Pk+1 follows as a consequence.
To get Pk+1 from Pk, we have to add on the next number after 3k-2, so let us add (3k+1) to both sides of the equation for Pk:
= (3k2-k+6k+2)/2
= (3k2+5k+2)/2
= Pk+1